이진트리란?
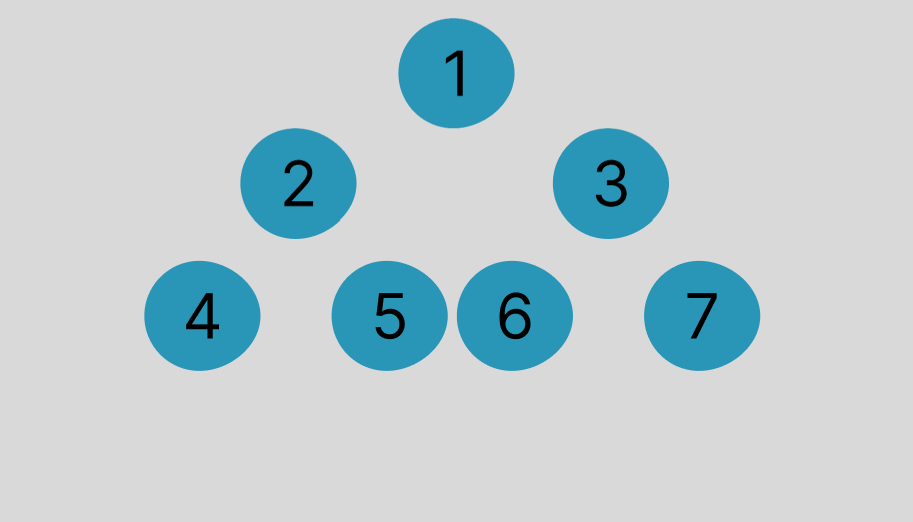
이진 트리는 루트(Root) 노드에서 시작하여 각 노드는 왼쪽 서브트리(Left Subtree)와 오른쪽 서브트리(Right Subtree)로 이루어져 있습니다. 각 노드의 자식 노드는 최대 두 개이기 때문에, 이진 트리는 가장 단순한 형태의 트리 중 하나입니다.
이진트리의 활용 분야
- 데이터베이스: 색인(Index)을 만드는 데 사용
- 정렬 알고리즘: 이진 탐색 트리(Binary Search Tree)
- 압축 알고리즘: 허프만 코딩(Huffman Coding)
- 인공지능: 의사결정나무(Decision Tree)
이진트리의 장단점
장점
- 검색 속도가 빠릅니다
- 데이터를 효율적으로 저장합니다
- 구현이 간단합니다
단점
- 균형이 맞지 않을 경우 성능이 저하됩니다
- 트리의 높이가 너무 높아질 수 있습니다
- 메모리 사용량이 많을 수 있습니다
이진트리의 순회 방법
1
/ \
2 3
/ \ / \
4 5 6 7
전위 순회 (Preorder)
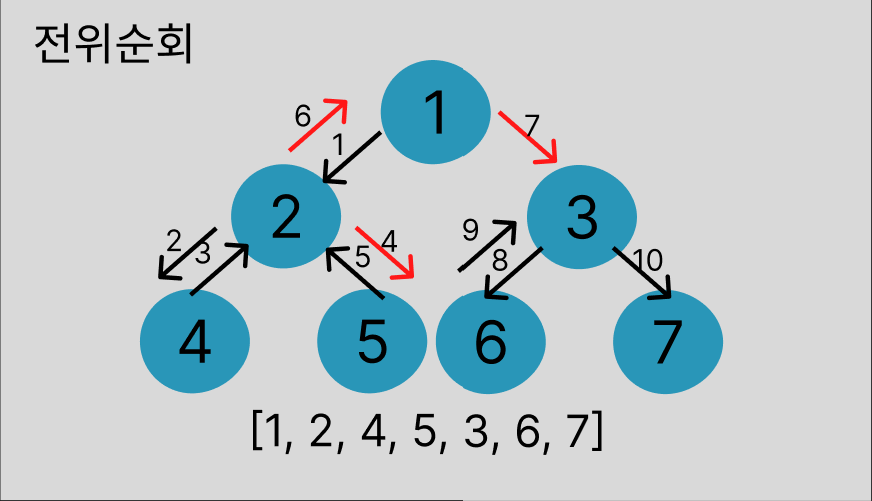
순서: 중앙 → 왼쪽 → 오른쪽
결과: 1 → 2 → 4 → 5 → 3 → 6 → 7
def pre_order(node):
print(node.data, end=' ') # 먼저 출력
if node.left_node is not None:
pre_order(tree[node.left_node])
if node.right_node is not None:
pre_order(tree[node.right_node])
전위는 print가 가장 먼저 나오기 때문에 전위
중위 순회 (Inorder)
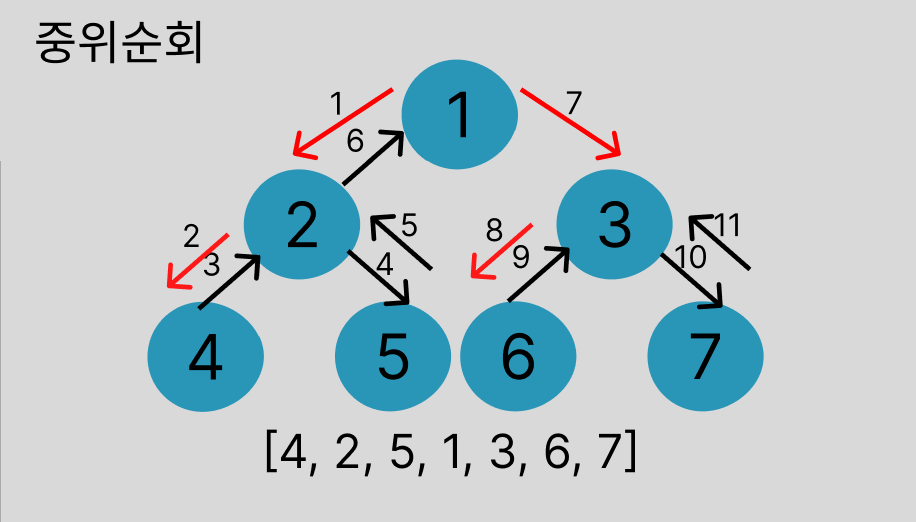
순서: 왼쪽 → 중앙 → 오른쪽
결과: 4 → 2 → 5 → 1 → 6 → 3 → 7
def in_order(node):
if node.left_node is not None:
in_order(tree[node.left_node])
print(node.data, end=' ') # 중간에 출력
if node.right_node is not None:
in_order(tree[node.right_node])
중위는 print가 중간에 나오기 때문에 중위
후위 순회 (Postorder)
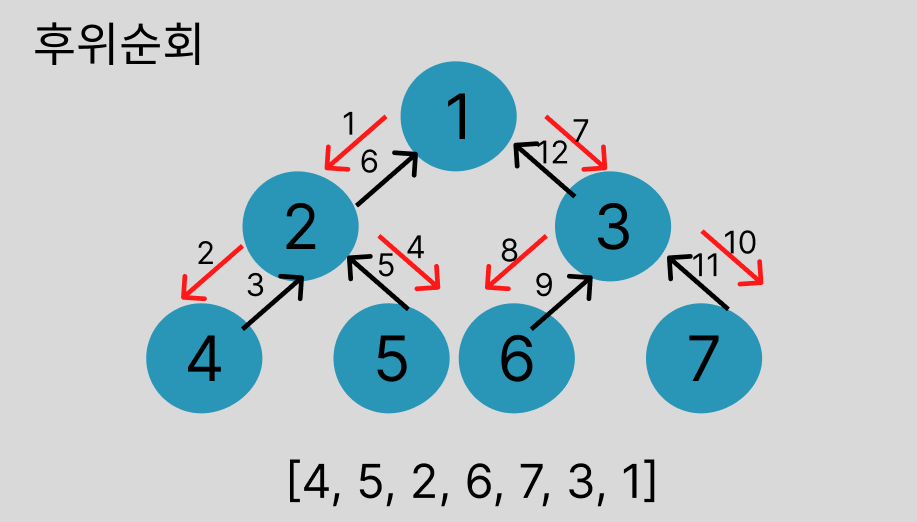
순서: 왼쪽 → 오른쪽 → 중앙
결과: 4 → 5 → 2 → 6 → 7 → 3 → 1
def post_order(node):
if node.left_node is not None:
post_order(tree[node.left_node])
if node.right_node is not None:
post_order(tree[node.right_node])
print(node.data, end=' ') # 마지막에 출력
후위는 print가 마지막에 나오기 때문에 후위
전체 코드
tree = {}
class Node:
def __init__(self, data, left_node, right_node):
self.data = data
self.left_node = left_node
self.right_node = right_node
def pre_order(node):
print(node.data, end=' ')
if node.left_node is not None:
pre_order(tree[node.left_node])
if node.right_node is not None:
pre_order(tree[node.right_node])
def in_order(node):
if node.left_node is not None:
in_order(tree[node.left_node])
print(node.data, end=' ')
if node.right_node is not None:
in_order(tree[node.right_node])
def post_order(node):
if node.left_node is not None:
post_order(tree[node.left_node])
if node.right_node is not None:
post_order(tree[node.right_node])
print(node.data, end=' ')
def solution(input):
for i in input:
cur, left, right = i
tree[cur] = Node(cur, left, right)
print('전위순회:', end=' ')
pre_order(tree[1])
print()
print('중위순회:', end=' ')
in_order(tree[1])
print()
print('후위순회:', end=' ')
post_order(tree[1])
print()
# 실행
solution([
[1, 2, 3],
[2, 4, 5],
[3, 6, 7],
[4, None, None],
[5, None, None],
[6, None, None],
[7, None, None]
])
출력 결과
전위순회: 1 2 4 5 3 6 7
중위순회: 4 2 5 1 6 3 7
후위순회: 4 5 2 6 7 3 1
핵심 정리
| 순회 방식 | 순서 | 외우는 방법 |
|---|---|---|
| 전위 순회 | 중앙 → 왼쪽 → 오른쪽 | print가 가장 먼저 |
| 중위 순회 | 왼쪽 → 중앙 → 오른쪽 | print가 중간에 |
| 후위 순회 | 왼쪽 → 오른쪽 → 중앙 | print가 마지막에 |